Расчет гравитационной постоянной G

Закон гравитационного взаимодействия гласит, сила гравитационного притяжения между двумя материальными точками массы, разделёнными расстоянием, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними. Гравитационная постоянная создаёт уравнение из этой взаимосвязи, это одна из важных универсальных констант природы. Чтобы определить эту константу, которая также была названа в честь Ньютона, в прошлом использовались исключительно механические методы, которые подвержены множеству искажений, поэтому G до сих пор применяется как константа с большой неточностью.

Для сравнения, неопределенность расчета обусловлена только точностью используемых естественных констант. В прошлом было несколько бесполезных попыток вычислить G[1]. Далее автор показывает на основе теории, созданной в [2], [3]. Основы новой возможности математического определения гравитационной постоянной.

Расчеты приводят к снижению неопределенности G на несколько порядков в пределах досягаемости. Первоначальное определение с помощью двух противоположных электронов на расстоянии r кажется очевидным. Аналогично закону Кулона, в котором заряды с разными знаками притягиваются друг к другу, гравитацию можно понимать как притяжение противоположных полюсов, в результате чего кулоновская сила F_c и гравитационная сила F_q сильно различаются по величине:

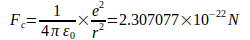
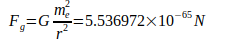
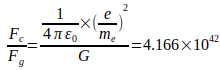
Отношение F_c ∕ F_g также называется числом Эддингтона, и даже для Фейнмана баланс сил между двумя взаимодействующими электронами имел большое значение. Отношение F_c ∕ F_g можно заменить на выражение N² ∕ 24, где N называется большим числом [2]. Прежде всего, предполагается, что 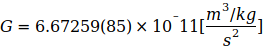признано Международным комитетом по кодатам в 1986 году [4].

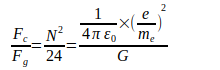
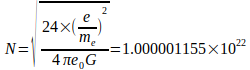(1)
Результат показывает, что Большое число N является большим числом около 1 X 10²². В 1986 году такие данные, как G= 6.672605 X 10^-11, были типичными, при этом большое число N= 1 X 10²² предполагалось без дальнейшего объяснения [3]. Отношение между массой и естественными константами определяется следующим образом: масса Планка соответствует M_o без π ∕ 2 Планка 1900 года. Z₀ - характеристическое сопротивление вакуума [3].

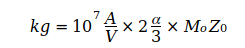
Эти уравнения соединяются с другими константами природы, а его расширение предлагает возможность определения G₀ в качестве основы для исходных данных для определения большого числа N₀. Далее буква b используется для постоянной тонкой структуры α.

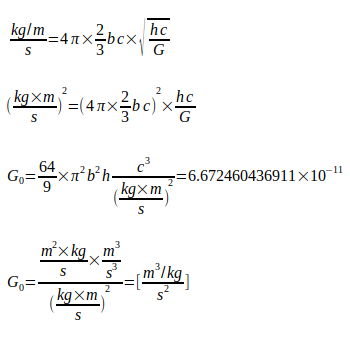 (2)
Индекс 0 в G₀ относится к использованию значения для дальнейших расчетов. После преобразования уравнения (1) получаем

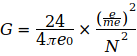
И с подстановкой 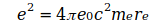получается абсолютно минимальный вариант уравнения для вычисления G:

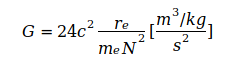 (3)
Приравнивая уравнение (3) к уравнению (2),N может быть получено следующим образом:

Индекс на N₀ указывает на основу для дальнейших расчетов. Относительная неопределенность N₀² связана с неопределенностью констант, связанных с 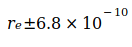, 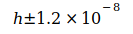и 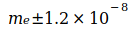, сумма которых равна 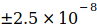. Кодата опубликовала следующие значения G в период с 1986 по 2014 год:

Таблица I

Значение кодата	Неопределенность	Дата
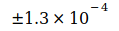		1986
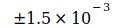		1998
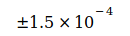		2002
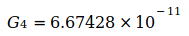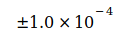		2006
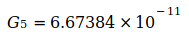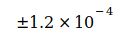		2010
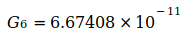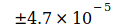		2014

Данные показывают, что G достиг максимума в 2006 году, который потом снова падал в следующие годы. Родилась идея, связать эту тенденцию со снижением массы электрона m_e, которая, согласно преобразованному уравнению (3), приводит к G, то есть 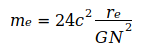. Эти величины были определены для точной оценки G₀ и N₀, приведенным в уравнении (2) и (4). Это приводит к следующим отклонениям для отдельных годовых значений:

Таблица II

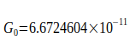	me-связанные отклонения
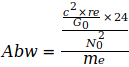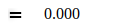		справочник
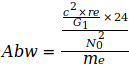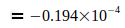		1986
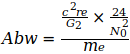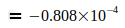		1998
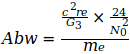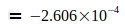		2002
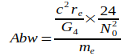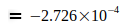		2006
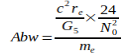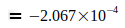		2010
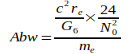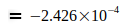		2014

Из этих отклонений, связанных с массой электронов, было установлено, что увеличение G, указанное Кодата, также связано с уменьшением m_e, определяемым уравнением (3). Трудно было найти единственную причину, о которой идет речь. В период с 1986 по 2014 год массы, сообщенные мне Кодата, были незначительно уменьшены на 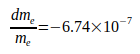. Таким образом, это может быть только кардинальная ошибка в определении G в 1986 году, которая будет устраняться в течение многих лет. Первые признаки появились из-за влияния совместного движения протона в атоме водорода, что широко обсуждается в специальной литературе.

Конечное тяжелое ядро движется под воздействием массы электрона вокруг общего центра тяжести, что приводит к поправке постоянной R_y Ридберга 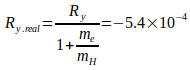. В то же время масса электрона увеличивается на его релятивистскую орбитальнаю скорость 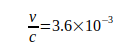, что оказывает влияние на другие переменные, которые являются неполными, чтобы быть обнаруженными [5].

Уменьшение постоянной Ридберга с R_y до R_yr также относится к массе электрона, а также к 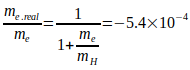. Для определения эффективной постоянной Ридберга R_yr используется частота водородного перехода, упомянутая Кодата в [6]: 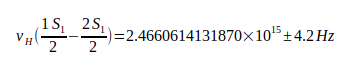(71).
Это приводит к реальной эффективной постоянной Ридберга R_yr:

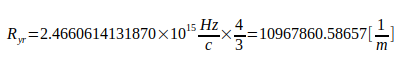
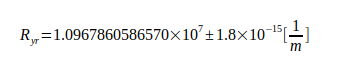
Постоянная Ридберга R_y считается самой точной естественной постоянной из всех известных. Безразмерное отношение Q между ним и действительной эффективной постоянной Ридберга является стержнем вычисления.
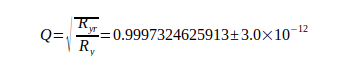(5)

Разница 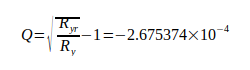соответствует отклонению связанному с m_e, показанному в таблице II. Сравнение показывает, что это отношение можно использовать для преодоления проблем, упомянутых при воспроизведении правильных соотношений для атома H, а также при определении G в соответствии с уравнением (3). Исходя из этого, гравитационная постоянная может быть рассчитана с использованием уравнений (3), (4), (5).

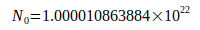
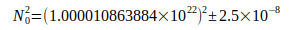
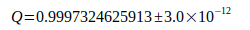
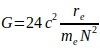
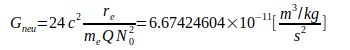(6)

Теперь мы рассмотрим, какие отклонения имеют достоверную информацию о G из литературы по сравнению с расчетным значением G_neu. Для этого в Таблице III для сравнения используются только достоверные значения, даже если они были вычислены несколько лет назад:

Таблица III

Номинал	Неопределенность	Источник	Год	Первоисточник
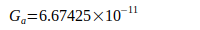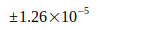		G World	1997	[7]
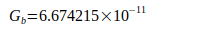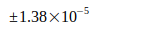		Uni Washington	2000	[7], [4]
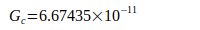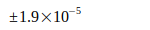		UCI-14 Input	2014	[6]
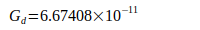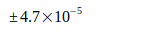		Codata values	2014	[6]

Как показано в следующей таблице IV, все отклонения этих значений от расчетного значения 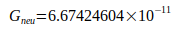находятся в пределах неопределенности, указанной авторами. Отношение рассчитанного отклонения к неопределенности составляет менее одного стандартного отклонения.

Таблица IV

Отношение	Отклонение	Девиация / Неопределенность
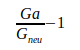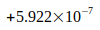		0.047
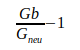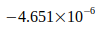		0.337
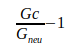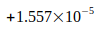		0.797
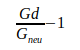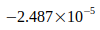		0.529

Сравнение результатов современных данных в соответствии с [7], таблица 7.5 с G_neu, показывает, что все допуски, указанные в них, соблюдаются. Это отличается от информации о G , приведенной Кодата в [6] таблице XV, где из 14 ссылок только следующие 5 соответствуют установленным для них допускам на погрешность:

Bagley and Luther (1997) LANL-97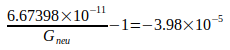
Gundlach and Merkowitz (2000, 2002)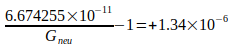
Kleinvoß, Kleinvoß et al. (2002)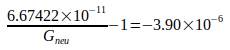
Schlamminger et al. (2006) UZur-06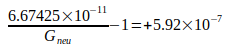
Newman et al. (2014) UCI-14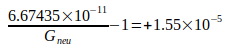

Таблица XV показывает, что некоторые значенияКодата подвержены значительным отклонениям. Это становится понятным, если использовать среднее из 14 содержащихся значений с 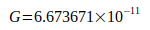вместо G_neu, где только 4 из 14 значений находятся в указанном диапазоне допуска.

Для практического расчета G имеет смысл объединить результаты, приведенные в уравнении (4) и уравнении (5), в постоянную K.

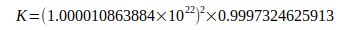
(7)

Из абсолютно минимального варианта уравнения (3) могут быть получены дополнительные уравнения путем замены радиуса r_e электрона один раз соотношением,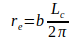 а затем соотношением: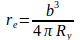

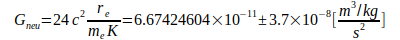
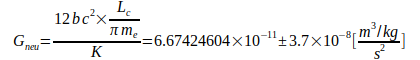
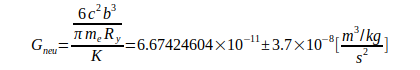
Неопределенность в расчете G в основном определяется N₀² согласно уравнению (4) или постоянной 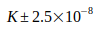согласно уравнению (7). Кроме того, в уравнении (3) добавлена неопределенность массы электрона 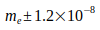. Неточностью постоянных, которые еще присутствуют, можно пренебречь. (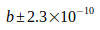, , 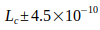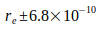). Таким образом, неопределенность массы электрона m_e определяет общую ошибку вычисления G.

Фактическая причина неточности m_e - основная постоянная Авогадро с 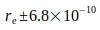, что ограничивает дальнейшее повышение точности G. В принципе, точность G ограничивается в 3 раза неопределенностью N_A. Благодаря усилиям СИ планируется приближение к 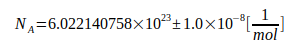[8], что указывает на будущие пределы точности G.

G-ПОЛЕ ЭТО ЭНЕРГИЯ! Следовательно, нет «пустого» пространства. ДАЖЕ ЭЛЕКТРОН ВНОСИТ СВОЙ ВКЛАД ..... (M. Geilhaupt)

Расчеты основаны на следующих константах:

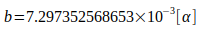
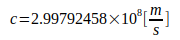
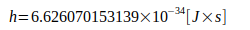
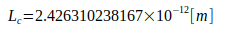
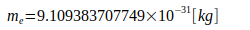
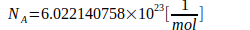
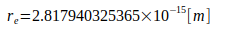
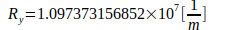
Литература

1.  E. Suckert: Über Natur des Elektrons und Ursache der Gravitation, 2013
2.  Prof. Dr. Manfred Geilhaupt: Fundamental Unit Momentum, 1986
3.  Prof. Dr. Manfred Geilhaupt: Basic Units of Physics, 1984
4.  Prof. Dr. Wolschin: Schwierige Bestimmung einer Naturkonstante, 2001
5.  Samuel Miesch: Atomare Spektren - Bohrsches Atom- Modell, 2003
6.  CODATA: Recommended Values of the Fundamental Physical Constants, 2014
7.  Ulf Kleinevoß: Bestimmung der Newtonschen Gravitationskonstante,2002
8.  David Newell: The CODATA 2017 values for the revision of the SI, 2018

Дипломированный инженер (FH) Kurt Vogell
Email: kurt.vogel@gmx.de
Дата:: 30.04.2019

 

Gravitational constant